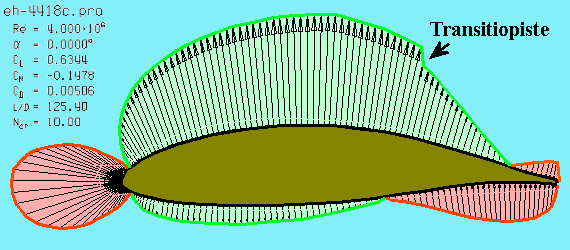
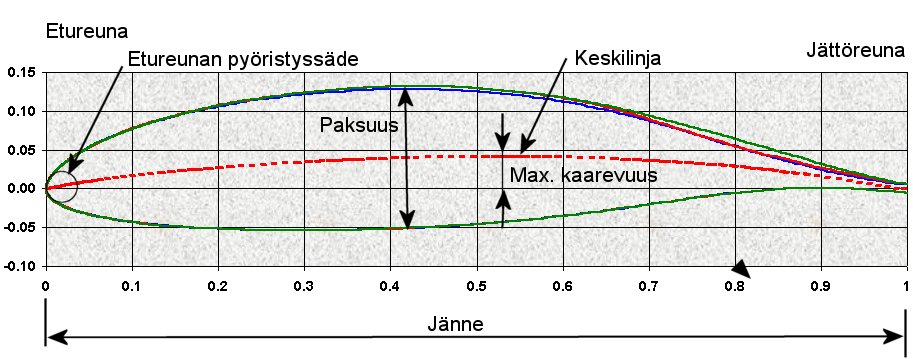
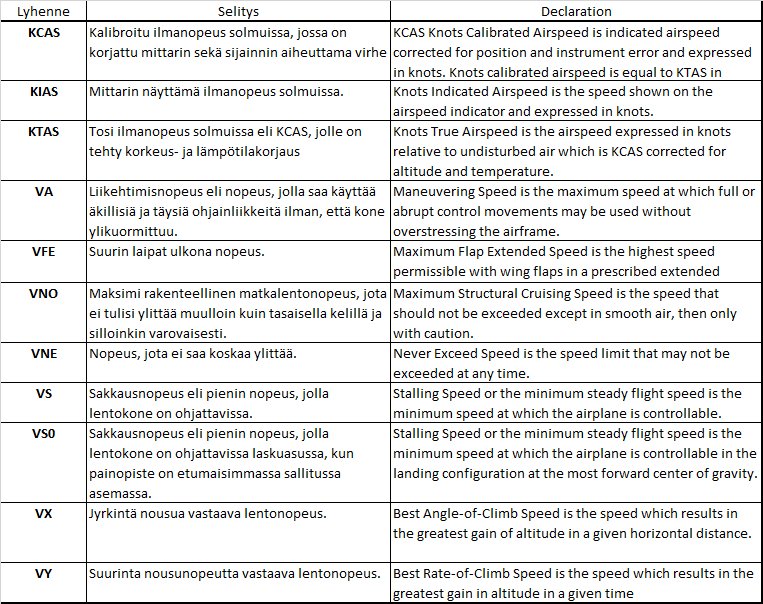
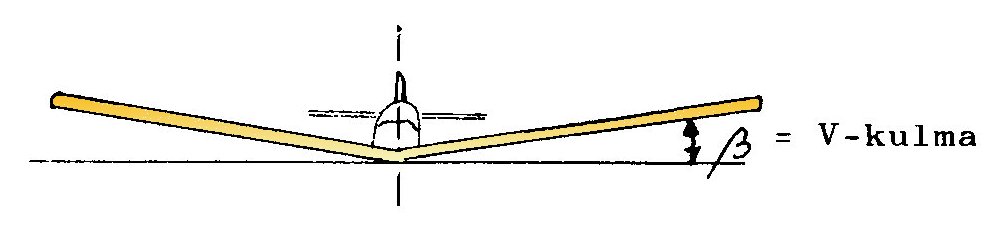
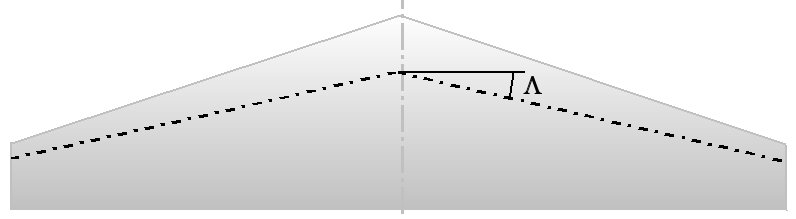
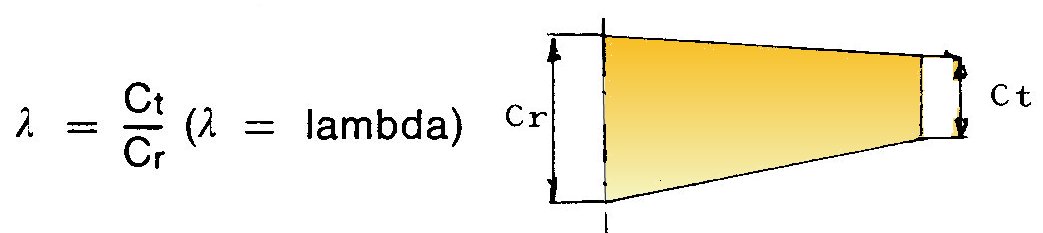
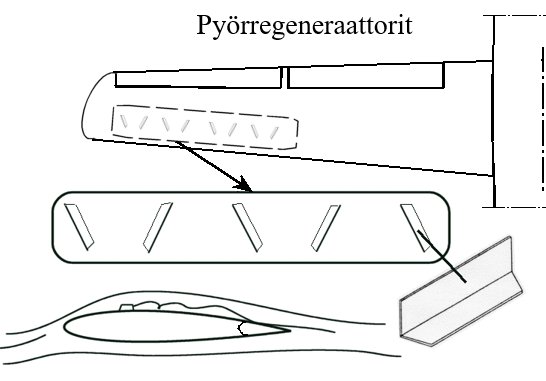
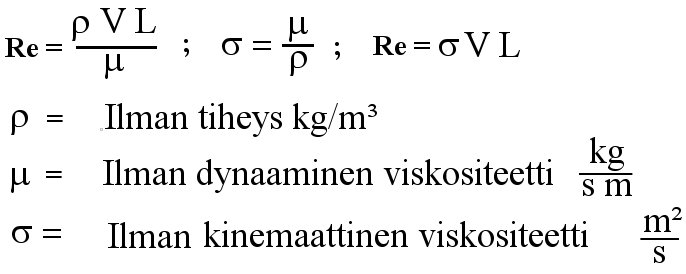5.2 Fysiikan lakeja

Tässä osiossa on aerodynamiikkaan liittyviä fysiikan lakeja sekä suureiden kuvauksia:

• Newtonin lait: Jatkuvuuslaki, dynamiikan peruslaki, voiman ja vastavoiman laki
• Bernoullin laki
• Aerodynamiikan kertoimet: Nostovoimakerroin, vastuskerroin, momenttikerroin
• Reynoldsin luku

Newtonin lait

Newtonin lait määrittelevät kappaleen sijainnin, nopeuden ja kiihtyvyyden. Ne ovat yleisiä luonnonlakeja, joita kaikki systeemit noudattavat. Aerodynamiikassa ilman ja lentokoneen keskinäiset vuorovaikutukset noudattavat näitä lakeja.

Newtonin ensimmäinen laki, jatkuvuuslaki

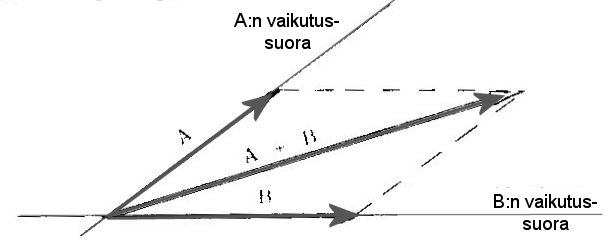
Kappale säilyttää liiketilansa, ellei mikään ulkoinen voima muuta sitä. Eli jos kappale on paikallaan, se ei ala liikkua tai, jos se liikkuu niin se jatkaa suoraa liikettä samalla nopeudella. Jos liikkuvaan kappaleeseen vaikuttaa voima, se vaikuttaa liikkeen suuntaan ja nopeuteen. Jos voimia on useampia, niiden kokonaisvaikutus on sama kuin yhden voiman, joka on kaikkien voimien vektorisumma.

Newtonin toinen laki, dynamiikan peruslaki

Kappaleen kiihtyvyys on suoraan verrannollinen vaikuttavaan voimaan ja kääntäen verrannollinen kappaleen massaan.  F = m a 

Newtonin kolmas laki, voiman ja vastavoiman laki

Jos kappale A työntää kappaletta B voimalla F, työntää kappale B kappaletta A yhtä suurella, mutta vastakkaissuuntaisella voimalla -F

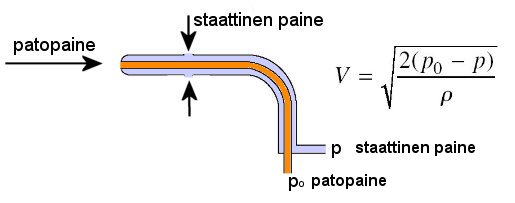
Bernoullin laki

Bernoullin laki pätee kitkattomalle ja kokoon puristumattomalle virtaukselle. Pitkin virtaputkea on staattisen paineen ja kineettisen paineen summa vakio eli P1 + ½ r V12 = P2 + ½ r V22

Tässä alaindeksit 1 ja 2 viittaavat peräkkäisiin kohtiin virtauksessa.

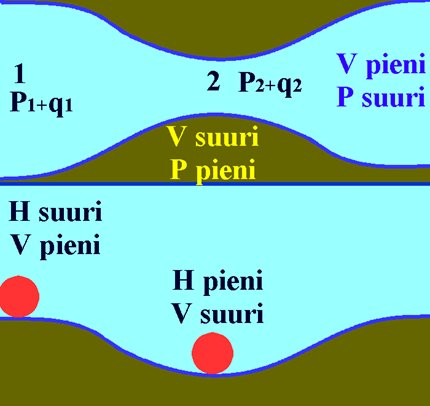Kuva: Bernoullin laki.

Bernoullin laki tarkoittaa sitä, että paine ja nopeus ovat keskenään vaihtokelpoisia energiamuotoja. Kuva havainnollistaa Bernoullin lakia, jossa ylempänä on esitetty venturiputki ja siinä vallitsevat olosuhteet laajennuksessa sekä kurkussa. Koska sama ilmamäärä kulkee putken lävitse, on ohuemmassa kohdassa virtauksen oltava nopeampaa, mistä seuraa paineen aleneminen. Kuvan alaosassa on verrattu tilannetta potentiaali- ja nopeusenergian säilyvyyden kanssa. Bernoullin lakia käytetään hyväksi esimerkiksi venturiputkessa, kaasuttimen kurkussa, alipainepumpuissa, nostovoiman syntyä selitettäessä jne. Bernoullin lain avulla voidaan päätellä virtaviivojen välisestä etäisyydestä kyseisessä kohdassa vallitseva paine ja virtausnopeus. Mitä kapeampi väli, sitä nopeampi virtaus ja pienempi paine.

Google: Bernoullin laki, Bernoulli’s law

Aerodynaamiset kertoimet

Aerodynaamisten kertoimien avulla muutetaan aerodynaamiset voimat dimensiottomiksi. Tällä tavalla voidaan kuvata ilmiöitä niiden koosta riippumatta ja käyttää samoja kaavoja sekä jumbojetin että hyttysen lennon kuvaamiseen. Luonnollisesti kertoimet ovat erilaisia, mutta kaavat säilyvät samoina olipa kyseessä jumbojetti tai hyttynen. Koska kertoimet ovat riippuvaisia Reynoldsin luvusta, kutakin Re-aluetta varten tarvitaan omat kertoimet, jotka esitetään yleensä kohtauskulmasta riippuvaisina taulukoina tai graafisina käyrästöinä. 

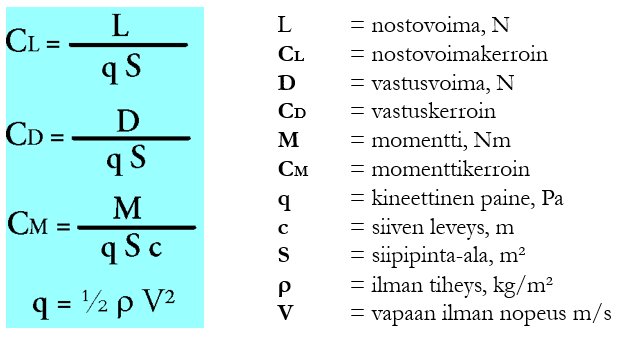Kaavat: Aerodynaamiset kertoimet ja niiden selitykset. Kertoimet ovat dimensiottomia suureita, jotka riippuvat Re-luvusta ja kohtauskulmasta.

Esimerkki Nostovoimakertoimesta:

Cherokee 140 lentää täydellä kuormalla (970 kg) laskuasussa nopeudella 87 km/h eli 24,1 m/s. Siipipinta-ala on 14,9 m2. Mikä on nostovoimakerroin CL?

Nostovoima on yhtä suuri kuin koneen paino eli L = m g = 970 x 9,81 = 9516 N

Kineettinen paine on q = ½ x 1,225 kg/m3 x 24,12 (m/s)2 = 355 Pa

Kerrottuna siipipinta-alalla saadaan 355 x 14,9 = 5300 N

CL = 9516/5300 = 1,79 mikä vastaa Cherokeen maksimi nostovoimakerrointa laipat ulkona.

Matkanopeudella 200 km/h eli 55,5 m/s saadaan nostovoimakertoimeksi 0,335.

Vastuskerroin

Vastuksen suuruutta voidaan kuvata paljaalla luvulla CD, joka on vastusvoima jaettuna kineettisen paineen ja siipipinta-alan tulolla.

Vastus jaetaan kahteen osaan: nostovoimasta riippuva vastus eli indusoitu vastus Di sekä haitallinen vastus Do, jota kutsutaan myös loisvastukseksi. Kokonaisvastus D on näiden summa

Kaava 3. Vastuskerroin voidaan jakaa indusoituun eli nostovoimasta riippuvaan osioon sekä haitalliseen vastukseen, joka johtuu esimerkiksi kitkasta ja jättöpyörteistä. Elliptisyys e riippuu siiven muodosta. Elliptisen siiven e = 1 ja muille muodoille tätä pienempi. Teoreettisesti elliptisen siiven liitosuhde on optimaalisin.

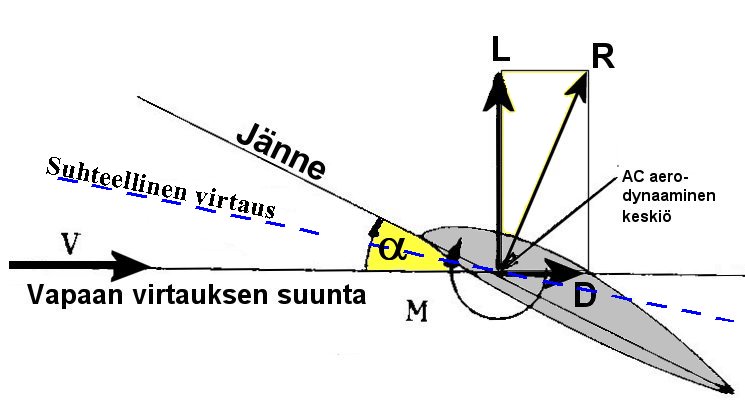
Siiven momenttikerroin CM

Momenttikerroin kuvaa siiven pyrkimystä kiertää koneen nokkaa joko ylös tai alas. Positiivinen momentti lisää kohtauskulmaa ja negatiivinen vähentää sitä. Momenttikerroin CM määritellään seuraavasti:

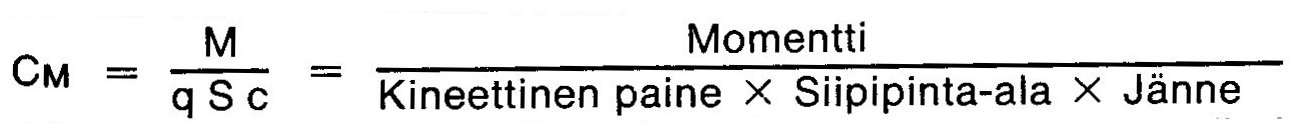Kaava: Momenttikerroin Momenttikerroin. Siiven aiheuttama momentti on normaalisti negatiivinen ja siksi koneen nokka pyrkii painumaan alas sitä enemmän mitä suuremmalla nopeudella lennetään. Korkeusohjain painaa pyrstöä alaspäin niin paljon, että saadaan kone vakautettua haluttuun lentoasentoon. Kaavassa jänteenä c käytetään keskimääräistä siiven leveyttä. Kaarevan profiilin momenttikerroin on negatiivinen eli se pyrii painamaan nokkaa alas päin. Symmetrisen profiilin tai S-muotoisen profiilin momenttikerroin on nolla tai lähes nolla. Koska siiven aiheuttama momentti pyrkii painamaan nokkaa alas eli pienentämään kohtauskulmaa, niin momenttikerroin on negatiivinen. Siiven nokkaa alas painava momentti tasapainotetaan korkeusperäsimen alas suuntautuvalla voimalla.

Esimerkki momentista:

Cherokee 140:n momenttikerroin CM = —0,06 ja siiven keskijänne c = 1,6 m. Tällöin saadaan nopeudella 200 km/t = 55,5 m/s seuraava momentti, joka painaa nokkaa alaspäin.

M = q S c CM  = ½ r V2 S c CM = - ½ x 1,225 x 55,52 x 14,9 x 1,6 x 0,06 = -2710 Nm = -267 kpm

Tämä momentti on tasapainotettava korkeusperäsimen vastamomentilla. Korkeusperäsimen nostovoimakeskiö on 4,25 m etäisyydellä siiven nostovoimakeskiöstä, joten tarvittava alaspäin suuntautuva peräsinvoima Fperäsin = 2710/4,25 = 638 N eli 65 kp.

Esimerkiksi laskusiivekkeiden käyttö lisää momenttikerrointa, mikä vaikuttaa selvästi koneen lentoasentoon ja vaatii sauvalla korjausta.

Reynoldsin luku, Re

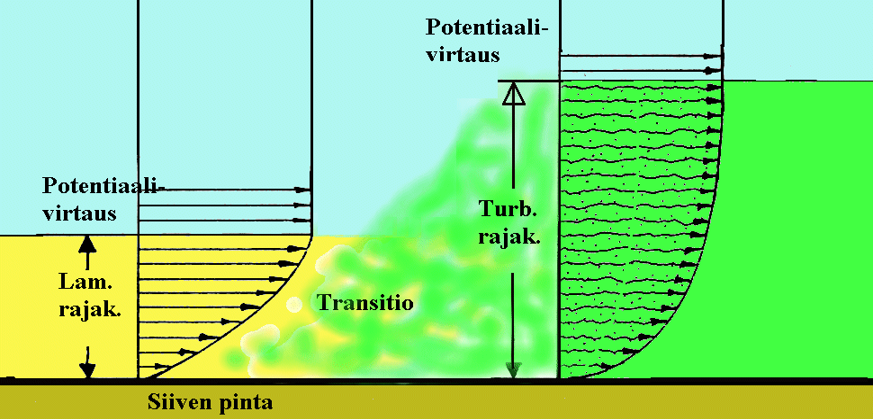
Ilman sisäinen kitka vaikuttaa sen käyttäytymiseen siten, että virtauksen luonne on riippuvainen ilman viskositeetista, virtauksessa olevan kappaleen muodosta ja dimensioista sekä virtausnopeudesta. Reynoldsin luku on dimensioton suure, joka kuvaa ilmamolekyyleihin kohdistuvien hitaus- ja kitkavoimien suhdetta. Jos tilannetta vastaava Re-luku on tunnettu sekä kyseistä Re-lukua vastaavat kertoimet, CL, CD ja CM ovat tunnettuja, niin voidaan laskea kappaleeseen kohdistuvat voimat ja momentit riippumatta kappaleen koosta.

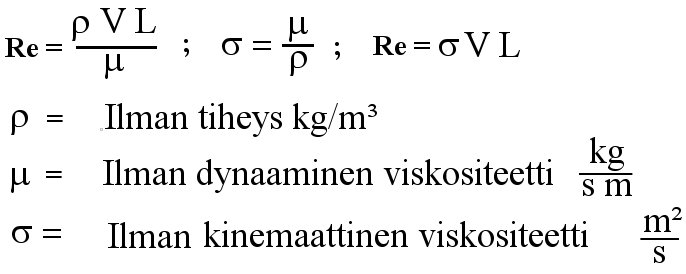Kaava: Reynoldsin luku määrittelee hitaus- ja kitkavoimien välisen suhteen. V = vapaan virtauksen nopeus [m/s], L = karakteristinen matka [m], joka esimerkiksi on siiven leveys ja putkivirtaukselle putken sisähalkaisija. On oleellista, että tulkittaessa käytetään samaa matkaa, jolla Re-luku on laskettu. Esimerkiksi rajakerrostarkasteluissa käytetään matkaa siiven etureunasta tarkastelukohtaan ja putkivirtauksissa matkana on putken halkaisija.

Reynoldsin lukualue siipiprofiilille vaihtelee runsaasti. Lennokeilla alue on 10 – 500 tuhatta, purjekoneella 1 – 3 miljoonaa, pienkoneella matkalennossa 3 – 5 miljoonaa, matkustajakoneella 10 – 50 miljoonaa. Kun saman muotoisen kappaleen ympäri tapahtuva virtaus tunnetaan tietyllä Re-luvulla, niin virtaus käyttäytyy samalla tavalla eri väliaineissa kaiken kokoisilla kappaleilla. Tällöin voidaan laskea mm. kappaleeseen vaikuttavat voimat ja momentit. 

Esimerkiksi nostovoima- ja vastuskertoimien kuvaajat ovat riippuvaisia Reynoldsin luvusta. Seuraavassa kuvassa on ilman ominaisuuksia, joita voi käyttää Re-lukua laskettaessa, kun ilman paine on 1013,25 hPa.

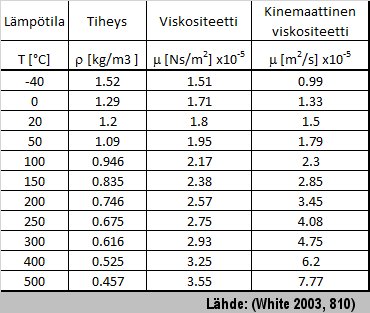Taulukko: Ilman viskositeetti merenpinnan paineessa Re-luvun laskentaa varten.

Reynoldsin luvun vaikutus nostovoimakertoimeen

 Re-luku vaikuttaa nostovoimakertoimeen eri kohtauskulmilla eri lailla. Seuraava kuva osoittaa erään 12% paksun profiilin nostovoimakertoimen riippuvuutta Re-luvusta.

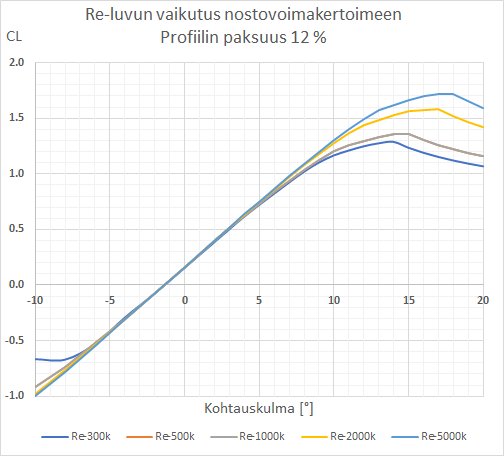Kuva. Re-luvun vaikutus 12% paksun profiilin nostovoimakertoimeen eri kohtauskulmilla.

Reynoldsin luvun vaikutus vastuskertoimeen

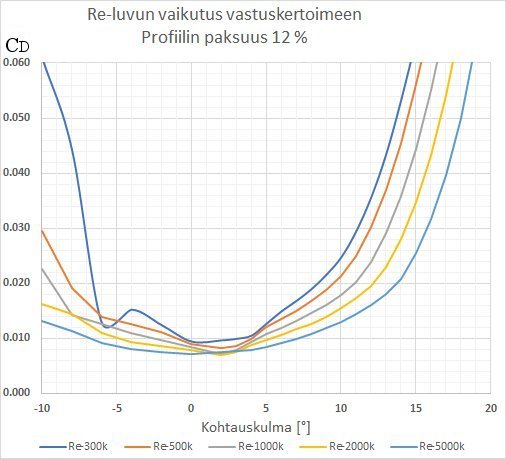Kuva. Re-luvun vaikutus 12% paksun profiilin vastuskertoimeen eri kohtauskulmilla. Korjaus; CL pitää olla CD

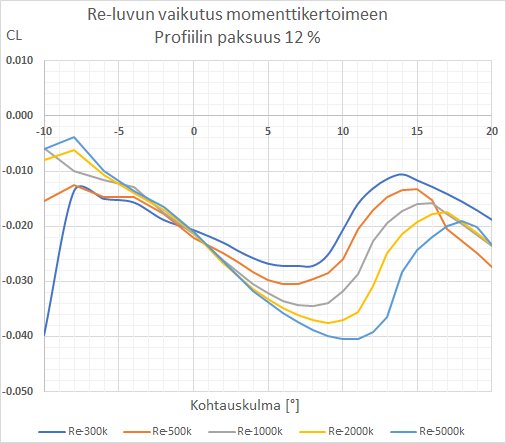
Reynoldsin luvun vaikutus momenttikertoimeen

Kuva. Re-luvun vaikutus 12% paksun profiilin momenttikertoimeen eri kohtauskulmilla.  Korjaus; CL pitää olla CM

Reynoldsin luvun vaikutus profiilin liitosuhteeseen

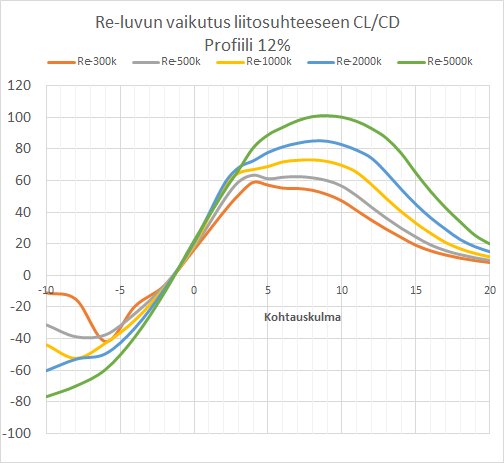Kuva. Re-luvun vaikutus 12% paksun profiilin liitosuhteeseen eri kohtauskulmilla. Huomaa erityisesti, että paras liitosuhde esiintyy eri kohtauskulmalla riippuen Re-luvusta. Tämä on erityisen tärkeää, kun on kyse lennokeista, joiden Re-luku on yleensä alle 500k.

5.3 Aerodynamiikan termejä

Tässä osiossa on esitetty aerodynamiikkaan liittyviä termejä sekä niiden määritelmiä

• Siipiprofiili ja siihen liittyvät nimitykset
• Lentonopeus, IAS, TAS ja GS
• V-kulma
• Nuolikulma
• Trapetsisuus
• Pyörregeneraattori

Siipiprofiili ja siihen liittyvät nimitykset

Siipiprofiililla tarkoitetaan siiven poikkileikkauksen muotoa. Siipiprofiilin geometristen suureiden nimitykset ilmenevät seuraavasta kuvasta.

Kuva: Siipiprofiiliin liittyvät nimitykset Profiilin päämitat ilmaistaan yleensä prosentteina jänteestä. Jänne = siiven leveys. Jänteen suunta osoittaa etureunasta keskelle jättöreunaa. Profiilin muotoa kuvaavia mittoja ovat: Etureunan pyöristyssäde, maksimi paksuus ja sen etäisyys etureunasta, maksimi kaarevuus ja sen paikan etäisyys etureunasta sekä jättöreunan paksuus. Profiilin muoto vaikuttaa sen ominaisuuksiin: Paksummalla profiililla on yleensä juoheammat sakkausominaisuudet ja suurempi vastus ja kohtuullisen hyvä nostovoimakerroin Suuri etureunan pyöristyssäde pehmentää sakkausominaisuuksia. Terävä etureuna johtaa helposti etureunasta alkavaan sakkaukseen, joka on arvaamaton ja vaikeasti hallittavissa. Kaarevuuden kasvu lisää maksimi nostovoimakerrointa ja nokka alas momenttia. Keskilinjan jättöreuna voi olla kääntynyt hieman yläviistoon, jolloin profiilia kutsutaan S-profiiliksi. Tämä vähentää nokka alas momenttia ja on siksi yleisesti käytetty "lentävissä siivissä", koska siten saadaan siipi stabiiliksi.

 Mitä kaarevampi profiili, sitä suurempi "nokka alas taipumus" eli momentti joka painaa koneen nokkaa alaspäin. Kaarevuus lisää profiilin maksiminostovoimaa. Maksimipaksuuden paikalla on merkitystä profiilin laminaarisuuden kannalta. Laminaariprofiililla on olemassa pienen vastuksen alue tietyllä nostovoimakertoimen alueella. Profiilin asento ja siihen vaikuttavat voimat virtauksessa nähdään seuraavasta kuvasta.

Kuva: Profiilin asento virtauksessa ja siihen liittyvät nimitykset. Kohtauskulma α on jänteen ja vapaan virtauksen välinen kulma. Nostovoima on kohtisuoraan vapaata virtausta vastaan ja vastus sen suuntainen. Momentti on positiivinen, kun se pyrkii kasvattamaan kohtauskulmaa eli nostamaan nokkaa. Profiilin asento määräytyy VAPAAN eli häiriintymättömän VIRTAUKSEN ja profiilin jänteen välisestä kulmasta. Tätä kulmaa nimitetään kohtauskulmaksi a. Nostovoiman L suunnaksi valitaan kohtisuora vapaata virtausta vastaan ja vastuksen D suunnaksi virtauksen suunta. Nostovoima- ja vastusvektorit piirretään aerodynaamiseen keskiöön AC:hen, jonka sijainti on noin 25 % jänteestä siiven etureunasta mitattuna. AERODYNAAMINEN KESKIÖ määritellään siten, että se on piste, jossa profiilin momentti ei muutu kohtauskulman muuttuessa. Tämä momentti M vaikuttaa aerodynaamiseen keskiöön ja on positiivinen silloin, kun se lisää kohtauskulmaa eli nostaa koneen nokkaa. Ylöspäin kaarevan profiilin momentti on negatiivinen eli se pyrkii painamaan nokkaa alas.    Lentonopeus, IAS, TAS ja GS Lentokoneen nopeuden ilmaisu vaatii referenssin, jonka suhteen nopeus ilmoitetaan. Lentokoneen nopeusmittari, joka on kytketty pitot-putkeen näyttää pitot-painetta vastaavaa nopeutta, joka vastaa lentokoneen aerodynaamisia ominaisuuksia kineettisen paineen avulla eli q = ½ r V2. Tämä paine-ero mitataan pitotputken päästä, jossa vallitsee pitot-paine ja pitot-putken sivusta, jossa vallitsee vapaan ilman paine eli staattinen paine. Lentotehtävän kannalta tärkeä nopeus on todellinen maanopeus, joka puolestaan on ilmanopeuden ja tuulen nopeuden vektorisumma.    Kuva. Nopeusmittari. IAS = vihreä asteikko. TAS = valkea asteikko, kun painekorkeus ja ilman lämpötila on asetettu nupilla mittaritaulun yläosassa kohdakkain vastaamaan reitin olosuhteita. Esimerkissä 7000 jalkaa ja 15°C. Ohjaaja säätää painekorkeuden ja nupilla ilman lämpötilan. Valkea asteikko osoittaa tosi ilmanopeuden. IAS = indikoitu lentonopeus (Indicated Air Speed) on lentokoneen nopeusmittarin näyttämä ilmanopeus, joka riippuu mm. ilman tiheydestä ja mittausjärjestelmän konfiguraatiosta. Perinteinen mittaus tapahtuu Pitot-putken välityksellä mitatusta patopaineen ja staattisen paineen erotuksesta. Nopeusmittausjärjestelmän virheet on pyritty korjaamaan enemmän tai vähemmän onnistuneesti, jotta IAS olisi mahdollisimman tarkka. Kaikki lentokoneen liikehdintään liittyvät ilmiöt noudattavat IAS:n mukaista nopeutta. Erityisesti on painotettava, että sakkausnopeuden on kaikilla korkeuksilla sama. TAS = Tosi lentonopeus (True Air Speed) tarkoittaa todellista ilmanopeutta, joka yleensä on suurempi kuin IAS, koska ilman tiheys laskee korkeuden mukana. TAS määritellään korjaamalla IAS:n arvoa painekorjauksen ja ilman lämpötilan avulla. Tosi ilmanopeutta käytetään mm. suunnistus­laskelmissa. GS = Maanopeus (Ground Speed) on nimensä mukaan lentokoneen nopeus maan suhteen. Maanopeus on tuulen ja TAS:n vektorisumma. GPS-paikannukseen perustuvat nopeus­mittarit näyttävät tosi maanopeuden, lentokorkeuden ja koordinaatit.   Nopeuslyhenteitä Lentonopeus voidaan ilmaista eri tavoin riippuen miten se on mitattu tai mihin tarkoitukseen sitä käytetään. Seuraavassa taulukossa on esimerkki erään koneen ohjekirjasta.    Taulukko. Nopeuslyhenteitä ja niiden käyttötarkoituksia. Koska lyhenteet perustuvat englannin kielisiin ilmaisuihin on englannin kielinen selostus rinnalla. 3 ensimmäistä ilmaisua liittyvät hetkelliseen lentonopeuteen ja lopput ilmaisuista liittyvät lentokoneen nopeusrajoituksiin. kts. Vn-diagrammi.

Siiven V-kulma

V-kulma ilmaisee siiven ja vaakatason välisen kulman. V-kulma parantaa koneen kallistus­vakavuutta. Teholliseen V-kulmaan lasketaan mukaan rungon vaikutus. Ylätasolla on positiivista V-kulmaa vaikka siivet olisivat vaakatasossa. Jos siiven kärjet ovat alempana kuin tyvi, niin V-kulma on negatiivinen tai sitä kutsutaan anhedraaliksi.

Kuva: V-kulma

Siiven nuolikulma

Nuolikulma Λ  ilmaisee, kuinka paljon siiven kärkiä on suunnattu taaksepäin. Nuolikulma määritellään jänteen 25 % linjasta kuvan osoittamalla tavalla. Nuolikulmaa käytetään parantamaan koneen suuntavakavuutta. Yliäänikoneessa käytetään suurta nuolikulmaa, jotta saadaan siipi "äänivallin" taakse.

Nuolikulma Λ on siiven 25 % viivan ja keskiviivaa vastaan kohtisuoran viivan välinen kulma.

Trapetsisuus

Trapetsisuus λ on siiven kärjen leveyden suhde tyven leveyteen. Se osoittaa siis, miten voimakkaasti kapenevasta siivestä on kysymys. Kaventamalla siiven kärkeä pienennetään indusoitua vastusta, mutta liiallinen kaventaminen lisää taipumusta kärkisakkaukseen.

Kuva. Trapetsisuus on siiven kärjen leveyden suhde tyven leveyteen. Pienentämällä trapetsisuutta pienen­netään indusoitua vastusta, mutta lisätään herkkyyttä kärkisakkaukseen. Cr Tyvijänne, Ct kärkijänne. Mitä kapeampi kärki sitä pienempi indusoitu vastus.

Pyörregeneraattori

Pyörregeneraattorit ovat pieniä n 5 - 10 cm pitkiä, pari kolme senttiä korkeita lipareita, jotka on asennettu esimerkiksi siiven yläpinnalle vähän ennen kohtaa, jossa virtaus irtoaisi ja sakkaus alkaisi. Sen tehtävänä on tuoda rajakerroksen yläpuolelta nopeampaa virtausta pintaan ja näin siirtää sakkauksen alkamista suuremmalle kohtauskulmalle ja parantaa nostovoimakertoimen maksimia. Pyörregeneraattorit asennetaan pareittain noin 15º kulmaan virtauksen suhteen muutaman sentin päähän toisistaan joko V- tai A-muotoon.

Pyörregeneraattori kiihdyttää rajakerroksen virtausta ja sallii suuremman kohtauskulman sekä parantaa nostovoimakerrointa ja kasvattaa sakkausnopeutta